gcop::Rn< _n > Class Template Reference

#include <rn.h>

Inheritance diagram for gcop::Rn< _n >:

Collaboration diagram for gcop::Rn< _n >:

List of all members.

Public Member Functions
	Rn (int n=_n)
void	Lift (Vectornd &v, const Vectornd &xa, const Vectornd &xb)
void	Retract (Vectornd &xb, const Vectornd &xa, const Vectornd &v)
void	dtau (Matrixnd &M, const Vectornd &v)
void	Adtau (Matrixnd &M, const Vectornd &v)
virtual bool	Bound (Vectornd &v, Vectornd &d, const Vectornd &v0)
virtual bool	Clip (Vectornd &v) const
Static Public Member Functions
static Rn< _n > &	Instance ()
Public Attributes
char	bndType
	type of bound
Vectornd	w
	ellipsoidal bound weights
Static Public Attributes
static const char	BND_BOX = 0
static const char	BND_ELLIPSOID = 1

---

Detailed Description

template<int _n = Dynamic>
class gcop::Rn< _n >

n-dimension vector space, i.e.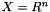

---

Constructor & Destructor Documentation

template<int _n>

gcop::Rn< _n >::Rn

(

int

n = _n

)

References gcop::Manifold< Matrix< double, _n, 1 >, _n >::lb, gcop::Manifold< Matrix< double, _n, 1 >, _n >::ub, and gcop::Rn< _n >::w.

---

Member Function Documentation

template<int _n>

void gcop::Rn< _n >::Adtau	(	Matrixnd &	M,
		const Vectornd &	v
	)		[virtual]

Adjoint map of the retraction, i.e. Ad((v))

Parameters:

M	resulting matrix operator
v	Lie algebra element

Reimplemented from gcop::Manifold< Matrix< double, _n, 1 >, _n >.

template<int _n>

bool gcop::Rn< _n >::Bound	(	Vectornd &	v,
		Vectornd &	d,
		const Vectornd &	v0
	)		[virtual]

Find a vector v = v0 + d for given v0 and d such that v satisfies the bounds; this is accomplished by modifying d appropriately and returning the updated v and d. Default implementation is assuming the bound is a box defined by the vectors lb and ub.

Parameters:

v	vector satisfying bounds
d	direction
v0	starting vector

Returns:

true on success, false if the arguments are not compatible

Referenced by gcop::Ddp< T, nx, nu, np >::Forward().

template<int _n>

bool gcop::Rn< _n >::Clip

(

Vectornd &

v

)

const [virtual]

Clips a vector to be within lb and ub

Parameters:

vector

v

Returns:

true if clipped

template<int _n>

void gcop::Rn< _n >::dtau	(	Matrixnd &	M,
		const Vectornd &	v
	)		[virtual]

Right-trivialized derivative of the retraction map dtau(v)

Parameters:

M	matrix operator
v	Lie algebra element

Reimplemented from gcop::Manifold< Matrix< double, _n, 1 >, _n >.

template<int _n>

Rn< _n > & gcop::Rn< _n >::Instance

(

)

[static]

Singleton to be used only for fixed-size Rn, i.e. Rn<n>::Instance()

Returns:

an instance of Rn<n>

template<int _n>

void gcop::Rn< _n >::Lift	(	Vectornd &	v,
		const Vectornd &	xa,
		const Vectornd &	xb
	)		[virtual]

Compute a lie algebra element corresponding to a group action between two given states on a manifold. This operation geometrically means that the curve from xa to xb is "lifted" to the tangent space of the manifold to a vector represented by the lie algebra element.

The element can also be regarded as a difference between the two states xa and xb. On a vector space this is v = xb - xa. On homogeneous manifolds v is a Lie algebra element corresponding to an action taking xa to xb.

Parameters:

v	Lie algebra element (regarded as difference between xb and xa)
xa	starting state
xb	ending state

Implements gcop::Manifold< Matrix< double, _n, 1 >, _n >.

template<int _n>

void gcop::Rn< _n >::Retract	(	Vectornd &	xb,
		const Vectornd &	xa,
		const Vectornd &	v
	)		[virtual]

Retracts a tangent vector on a manifold at state xa to produce a new state xb. The vector is represented using a Lie algebra element.

The operation can also be regarded as a way to perform addition on manifolds, i.e. to increment a given state xa by v to get a new state xb. On a vector space this is xb = xa + v. On homogeneous manifolds v is a Lie algebra element corresponding to an action taking xa to xb.

Parameters:

xb	ending state
xa	starting state
v	Lie algebra element (regarded as difference between xb and xa)

Implements gcop::Manifold< Matrix< double, _n, 1 >, _n >.

---

Member Data Documentation

template<int _n = Dynamic>

const char gcop::Rn< _n >::BND_BOX = 0 [static]

template<int _n = Dynamic>

const char gcop::Rn< _n >::BND_ELLIPSOID = 1 [static]

template<int _n = Dynamic>

char gcop::Rn< _n >::bndType

type of bound

template<int _n = Dynamic>

Vectornd gcop::Rn< _n >::w

ellipsoidal bound weights

Referenced by gcop::Rn< _n >::Rn().

---

The documentation for this class was generated from the following file:

• lib/systems/manifolds/rn.h