#include <group.h>

Inheritance diagram for gcop::Group< n, m >:

Collaboration diagram for gcop::Group< n, m >:

Public Member Functions
virtual void	inv (Matrixmd &gi, const Matrixmd &g) const
virtual Matrixmd	inv (const Matrixmd &g) const
virtual void	diff (Matrixmd &dg, const Matrixmd &ga, const Matrixmd &gb) const
virtual Matrixmd	diff (const Matrixmd &ga, const Matrixmd &gb) const
virtual void	hat (Matrixmd &g, const Vectornd &v) const =0
virtual Matrixmd	hat (const Vectornd &v) const
virtual void	hatinv (Vectornd &v, const Matrixmd &g) const =0
virtual Vectornd	hatinv (const Matrixmd &g) const
virtual void	Tg (Matrixnd &M, const Matrixmd &g) const =0
virtual Matrixnd	Tg (const Matrixmd &g) const
virtual void	Ad (Matrixnd &M, const Matrixmd &g) const =0
virtual Matrixnd	Ad (const Matrixmd &g) const
virtual void	ad (Matrixnd &M, const Vectornd &v) const =0
virtual Matrixnd	ad (const Vectornd &v) const
virtual void	adinv (Vectornd &v, const Matrixnd &M) const =0
virtual Vectornd	adinv (const Matrixnd &M) const
virtual void	exp (Matrixmd &g, const Vectornd &v) const =0
virtual Matrixmd	exp (const Vectornd &v) const
virtual void	log (Vectornd &v, const Matrixmd &g) const =0
virtual Vectornd	log (const Matrixmd &g) const
virtual void	cay (Matrixmd &g, const Vectornd &v) const
virtual Matrixmd	cay (const Vectornd &v) const
virtual void	cayinv (Vectornd &v, const Matrixmd &g) const
virtual Vectornd	cayinv (const Matrixmd &g) const
virtual void	dcay (Matrixnd &M, const Vectornd &v) const =0
virtual Matrixnd	dcay (const Vectornd &v) const
virtual void	dcayinv (Matrixnd &M, const Vectornd &v) const =0
virtual Matrixnd	dcayinv (const Vectornd &v) const
virtual void	Lift (Vectornd &v, const Matrixmd &ga, const Matrixmd &gb)
virtual void	Retract (Matrixmd &gb, const Matrixmd &ga, const Vectornd &v)
virtual void	dtau (Matrixnd &M, const Vectornd &v)
virtual void	Adtau (Matrixnd &M, const Vectornd &v)
Static Public Attributes
static const Matrixmd	Id = Matrix<double, m, m>::Identity()
static const Vectornd	e = Matrix<double, n, 1>::Zero()

Detailed Description

template<int n, int m>
class gcop::Group< n, m >

General definition of a matrix Lie group and its algebra. Defines basic operations such as identity, inverse, multiplication, maps and flows from algebra to the group using exponentiation, adjoint transform and operators. This should serve as a base class for implementing specific groups.

A Lie group is also a homogeneous manifold, so it subclasses Manifold and provides a default implementation of the operations Manifold::Lift and Manifold::Retract

Subclasses should provide all methods (inv, cay, cayinv are provided for convenience but they can be implemented more efficiently for specific groups)

Parameters:

n	manifold dimension, i.e. algebra alements are vectors 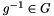$v\in R^n$
m	matrix dimension, group elements are m-by-m matrices 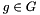$g \in G \subset GL(m)$

Member Function Documentation

template<int n, int m>

virtual void gcop::Group< n, m >::Ad	(	Matrixnd &	M,
		const Matrixmd &	g
	)		const `[pure virtual]`

The operator 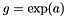$\operatorname{Ad}_g:\mathfrak{g}\rightarrow\mathfrak{g}$ . One can think of this operator as a change-of-frame transformation.

Parameters:

m	resulting transformation
g	group element corresponding to frame change

template<int n, int m>

Matrix< double, n, n > gcop::Group< n, m >::Ad ( const Matrixmd & g ) const [virtual]

The operator 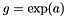$\operatorname{Ad}_g:\mathfrak{g}\rightarrow\mathfrak{g}$ . One can think of this operator as a change-of-frame transformation.

Returns:: resulting transformation

Parameters:

g	group element corresponding to frame change

template<int n, int m>

virtual void gcop::Group< n, m >::ad	(	Matrixnd &	M,
		const Vectornd &	v
	)		const `[pure virtual]`

The operator 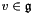$\operatorname{ad}_\xi:\mathfrak{g}\rightarrow\mathfrak{g}$ . One can think of this operator as the infinitesimal of the change-of-frame transformation. It can also be written using brackets [*,*].

Parameters:

m	resulting map
a	argument

template<int n, int m>

Matrix< double, n, n > gcop::Group< n, m >::ad ( const Vectornd & v ) const [virtual]

The operator 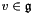$\operatorname{ad}_\xi:\mathfrak{g}\rightarrow\mathfrak{g}$ . One can think of this operator as the infinitesimal of the change-of-frame transformation. It can also be written using brackets [*,*].

Returns:: resulting map

Parameters:

a argument

template<int n, int m>

virtual void gcop::Group< n, m >::adinv	(	Vectornd &	v,
		const Matrixnd &	M
	)		const `[pure virtual]`

Inverse of ad operator

Parameters:

v	resulting algebra element
m	ad operator matrix

template<int n, int m>

Matrix< double, n, 1 > gcop::Group< n, m >::adinv ( const Matrixnd & M ) const [virtual]

Inverse of ad operator

Returns:: resulting algebra element

Parameters:

m	ad operator matrix

template<int n, int m>

void gcop::Group< n, m >::Adtau	(	Matrixnd &	M,
		const Vectornd &	v
	)		`[virtual]`

template<int n, int m>

void gcop::Group< n, m >::cay	(	Matrixmd &	g,
		const Vectornd &	v
	)		const `[virtual]`

Cayley map of a lie algebra element a 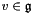$g=\text{cay}(a)$ . Subclasses should implement this method

Parameters:

g	resulting group element 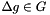$g \in G$
v	Lie algebra element 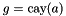$v\in\mathfrak{g}$

template<int n, int m>

Matrix< double, m, m > gcop::Group< n, m >::cay ( const Vectornd & v ) const [virtual]

Cayley map of a lie algebra element a 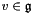$g=\text{cay}(a)$ . Subclasses should implement this method

Returns:: resulting group element $g \in G$

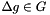
Parameters:

v	Lie algebra element 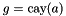$v\in\mathfrak{g}$

template<int n, int m>

void gcop::Group< n, m >::cayinv	(	Vectornd &	v,
		const Matrixmd &	g
	)		const `[virtual]`

Inverse of cayley 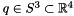$v=\text{cay}^{-1}(g)$ . Subclasses should implement this method

Parameters:

v	Lie algebra element 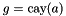$v\in\mathfrak{g}$
g	group element 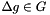$g \in G$

Referenced by gcop::MbsCspace::Lift(), and gcop::MbsManifold::Lift().

template<int n, int m>

Matrix< double, n, 1 > gcop::Group< n, m >::cayinv ( const Matrixmd & g ) const [virtual]

Inverse of cayley 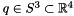$v=\text{cay}^{-1}(g)$ . Subclasses should implement this method

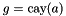
Returns:: v Lie algebra element $v\in\mathfrak{g}$

Parameters:

g	group element 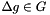$g \in G$

template<int n, int m>

virtual void gcop::Group< n, m >::dcay	(	Matrixnd &	M,
		const Vectornd &	v
	)		const `[pure virtual]`

Right-trivialized tangent of cayley

Parameters:

m	resulting linear map
v	Lie algebra element 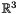$v\in\mathfrak{g}$

template<int n, int m>

Matrix< double, n, n > gcop::Group< n, m >::dcay ( const Vectornd & v ) const [virtual]

Right-trivialized tangent of cayley

Returns:: resulting linear map

Parameters:

v	Lie algebra element 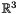$v\in\mathfrak{g}$

template<int n, int m>

virtual void gcop::Group< n, m >::dcayinv	(	Matrixnd &	M,
		const Vectornd &	v
	)		const `[pure virtual]`

Right-trivialized tangent inverse of cayley

Parameters:

m	resulting linear map
v	Lie algebra element 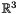$v\in\mathfrak{g}$

template<int n, int m>

Matrix< double, n, n > gcop::Group< n, m >::dcayinv ( const Vectornd & v ) const [virtual]

Right-trivialized tangent inverse of cayley

Returns:: resulting linear map

Parameters:

v	Lie algebra element 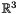$v\in\mathfrak{g}$

template<int n, int m>

void gcop::Group< n, m >::diff	(	Matrixmd &	dg,
		const Matrixmd &	ga,
		const Matrixmd &	gb
	)		const `[virtual]`

Compute the difference b/n two elements 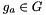$\Delta g=g_a^{-1}g_b$ .

Parameters:

dg	resulting group element 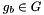$\Delta g \in G$
ga	first group element 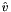$g_a \in G$
gb	second group element 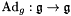$g_b \in G$

Referenced by gcop::GunicycleManifold::Lift().

template<int n, int m>

Matrix< double, m, m > gcop::Group< n, m >::diff	(	const Matrixmd &	ga,
		const Matrixmd &	gb
	)		const `[virtual]`

Compute the difference b/n two elements 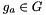$\Delta g=g_a^{-1}g_b$ .

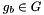
Returns:: resulting group element $\Delta g \in G$

Parameters:

ga	first group element 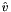$g_a \in G$
gb	second group element 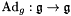$g_b \in G$

template<int n, int m>

void gcop::Group< n, m >::dtau	(	Matrixnd &	M,
		const Vectornd &	v
	)		`[virtual]`

template<int n, int m>

virtual void gcop::Group< n, m >::exp	(	Matrixmd &	g,
		const Vectornd &	v
	)		const `[pure virtual]`

Exponentiate lie algebra element a 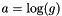$g=\exp(a)$ . Subclasses should implement this method

Parameters:

g	resulting group element 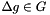$g \in G$
v	Lie algebra element 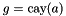$v\in\mathfrak{g}$

template<int n, int m>

Matrix< double, m, m > gcop::Group< n, m >::exp ( const Vectornd & v ) const [virtual]

Exponentiate lie algebra element a 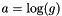$g=\exp(a)$ . Subclasses should implement this method

Returns:: resulting group element $g \in G$

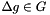
Parameters:

v	Lie algebra element 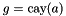$v\in\mathfrak{g}$

template<int n, int m>

virtual void gcop::Group< n, m >::hat	(	Matrixmd &	g,
		const Vectornd &	v
	)		const `[pure virtual]`

The operator 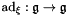$\hat v$ such that $(v) I + v$

Parameters:

g	resulting map
v	given algebra element

template<int n, int m>

Matrix< double, m, m > gcop::Group< n, m >::hat ( const Vectornd & v ) const [virtual]

The operator 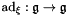$\hat v$ such that $(v) I + v$

Returns:: resulting map

Parameters:

v	given algebra element

template<int n, int m>

virtual void gcop::Group< n, m >::hatinv	(	Vectornd &	v,
		const Matrixmd &	g
	)		const `[pure virtual]`

Inverse of hat operator

Parameters:

v	resulting algebra element
g	infinetisamal group element

template<int n, int m>

Matrix< double, n, 1 > gcop::Group< n, m >::hatinv ( const Matrixmd & g ) const [virtual]

Inverse of hat operator

Returns:: resulting algebra element

Parameters:

g	infinetisamal group element

template<int n, int m>

void gcop::Group< n, m >::inv	(	Matrixmd &	gi,
		const Matrixmd &	g
	)		const `[virtual]`

Compute the inverse of a given group element

Parameters:

gi	inverse 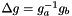$g^{-1} \in G$
g	group element 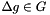$g \in G$

template<int n, int m>

Matrix< double, m, m > gcop::Group< n, m >::inv ( const Matrixmd & g ) const [virtual]

Compute the inverse of a given group element

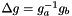
Returns:: inverse $g^{-1} \in G$

Parameters:

g	group element 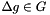$g \in G$

template<int n, int m>

void gcop::Group< n, m >::Lift	(	Vectornd &	v,
		const Matrixmd &	ga,
		const Matrixmd &	gb
	)		`[virtual]`

template<int n, int m>

virtual void gcop::Group< n, m >::log	(	Vectornd &	v,
		const Matrixmd &	g
	)		const `[pure virtual]`

Logarithm of a group element 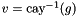$a = \log(g)$ . Subclasses should implement this method

Parameters:

v	Lie algebra element 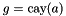$v\in\mathfrak{g}$
g	group element 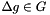$g \in G$

template<int n, int m>

Matrix< double, n, 1 > gcop::Group< n, m >::log ( const Matrixmd & g ) const [virtual]

Logarithm of a group element 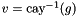$a = \log(g)$ . Subclasses should implement this method

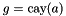
Returns:: v Lie algebra element $v\in\mathfrak{g}$

Parameters:

g	group element 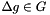$g \in G$

template<int n, int m>

void gcop::Group< n, m >::Retract	(	Matrixmd &	gb,
		const Matrixmd &	ga,
		const Vectornd &	v
	)		`[virtual]`

template<int n, int m>

virtual void gcop::Group< n, m >::Tg	(	Matrixnd &	M,
		const Matrixmd &	g
	)		const `[pure virtual]`

Tangent action

Parameters:

m	resulting action as a matrix
g	infinetisamal group element

template<int n, int m>

Matrix< double, n, n > gcop::Group< n, m >::Tg ( const Matrixmd & g ) const [virtual]

Tangent action

Returns:: resulting tangent action as a matrix

Parameters:

g	infinetisamal group element

Member Data Documentation

template<int n, int m>

Matrix< double, n, 1 > const gcop::Group< n, m >::e = Matrix<double, n, 1>::Zero() [static]

template<int n, int m>

Matrix< double, m, m > const gcop::Group< n, m >::Id = Matrix<double, m, m>::Identity() [static]

Referenced by gcop::SE3::dcayinv(), and gcop::Gcay().

The documentation for this class was generated from the following file:

lib/utils/group.h

Public Member Functions

Static Public Attributes

Detailed Description

template<int n, int m> class gcop::Group< n, m >

Member Function Documentation

Member Data Documentation

template<int n, int m>
class gcop::Group< n, m >