#include <flatoutputtparam.h>

Inheritance diagram for gcop::FlatOutputTparam< T, nx, nu, np, _ntp >:

Collaboration diagram for gcop::FlatOutputTparam< T, nx, nu, np, _ntp >:

Public Member Functions
	FlatOutputTparam (System< T, nx, nu, np > &sys, int ny_, int numberofknots_, int numberofderivatives_=0, bool fixfinal_=false)
bool	To (Vectorntpd &s, const vector< double > &ts, const vector< T > &xs, const vector< Vectorcd > &us, const Vectormd *p=0)
bool	From (vector< double > &ts, vector< T > &xs, vector< Vectorcd > &us, const Vectorntpd &s, Vectormd *p=0)
Public Attributes
int	numberofderivatives
	Number of derivatives of flat outputs needed.
int	numberofknots
	Number of knots for bezier curve.
int	ny
	Number of flat outputs.
vector< vector< VectorXd > >	knotsforallderivatives
	Knots for each derivative are computed on the fly.
bool	fixfinal
	should the final flat output be fixed (with necessary flatoutput time derivatives == 0)
Protected Member Functions
VectorXd	DeCasteljau (vector< VectorXd > &s, double u, int start, int end)
void	Createknotsforallderivatives (const Vectorntpd &s)

Detailed Description

template<typename T, int nx, int nu, int np = Dynamic, int _ntp = Dynamic>
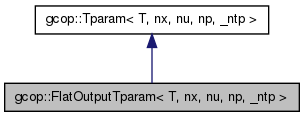
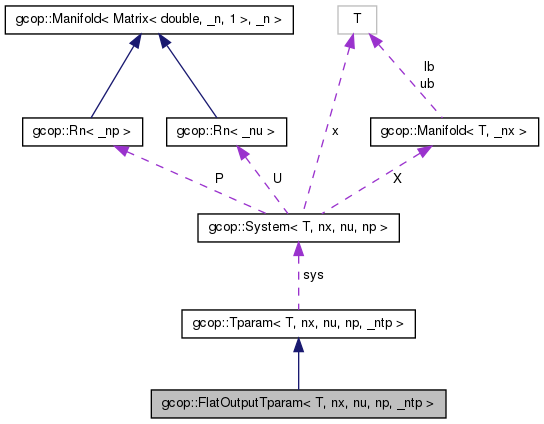
class gcop::FlatOutputTparam< T, nx, nu, np, _ntp >

This is a flat output parametrization class. The template vector ny gives the size of flat output TODO If ny Dynamic somehow resize all the knotvector sizes

Constructor & Destructor Documentation

template<typename T , int nx, int nu, int np, int _ntp>

gcop::FlatOutputTparam< T, nx, nu, np, _ntp >::FlatOutputTparam	(	System< T, nx, nu, np > &	sys,
		int	ny_,
		int	numberofknots_,
		int	numberofderivatives_ = `0`,
		bool	fixfinal_ = `false`
	)

Constructor

Parameters:

sys	System used for manifold
numberofknots	The number of knots used for bezier curve. This also determines the degree of the curve
numberofderivatives_	The number of derivatives needed by the system for evaluating flat outputs

References gcop::FlatOutputTparam< T, nx, nu, np, _ntp >::knotsforallderivatives, gcop::FlatOutputTparam< T, nx, nu, np, _ntp >::numberofderivatives, gcop::FlatOutputTparam< T, nx, nu, np, _ntp >::numberofknots, and gcop::FlatOutputTparam< T, nx, nu, np, _ntp >::ny.

Member Function Documentation

template<typename T , int nx, int nu, int np = Dynamic, int _ntp = Dynamic>

void gcop::FlatOutputTparam< T, nx, nu, np, _ntp >::Createknotsforallderivatives ( const Vectorntpd & s ) [inline, protected]

This function evaluates all the knots Dk_i for all the derivatives needed This is dont recursively as noted in http://www.cs.mtu.edu/~shene/COURSES/cs3621/NOTES/spline/Bezier/bezier-der.html

Parameters:

s	The input knots

template<typename T , int nx, int nu, int np = Dynamic, int _ntp = Dynamic>

VectorXd gcop::FlatOutputTparam< T, nx, nu, np, _ntp >::DeCasteljau	(	vector< VectorXd > &	s,
		double	u,
		int	start,
		int	end
	)		`[inline, protected]`

Evaluate Bezier curve using knots in s using DeCasteljau algorithm

Parameters:

u	input point where bezier curve is evaluated (0,1)
start	Starting point for recursionP_0
end	ending point for recursion P_n

template<typename T , int nx, int nu, int np, int _ntp>

bool gcop::FlatOutputTparam< T, nx, nu, np, _ntp >::From	(	vector< double > &	ts,
		vector< T > &	xs,
		vector< Vectorcd > &	us,
		const Vectorntpd &	s,
		Vectormd *	p = `0`
	)		`[virtual]`

Convert from trajectory (ts,xs,us,p) to parameters s

Parameters:

ts	times
xs	states
us	controls
s	trajectory parametrization vector
p	system parameters (optional)

Returns:: true if conversion was successful

Reimplemented from gcop::Tparam< T, nx, nu, np, _ntp >.

template<typename T , int nx, int nu, int np, int _ntp>

bool gcop::FlatOutputTparam< T, nx, nu, np, _ntp >::To	(	Vectorntpd &	s,
		const vector< double > &	ts,
		const vector< T > &	xs,
		const vector< Vectorcd > &	us,
		const Vectormd *	p = `0`
	)		`[virtual]`