#include <heli.h>

Inheritance diagram for gcop::Heli:

Collaboration diagram for gcop::Heli:

Public Member Functions
	Heli ()
Public Attributes
double	rt
	distance from center of mass to main rotor (top)
double	rb
	distance from center of mass to rear rotor (back)

Detailed Description

Idealized small helicopter modelled as a rigid body with 6 degrees of freedom and 6 velocities and 4 control variables. The heli position is denoted 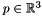$p \in \mathbb{R}^3$ , orientation 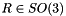$R \in SO(3)$ parametrized using roll 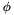$\phi$ , pitch 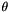$\theta$ , and yaw 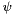$\psi$ . The linear velocity is denoted 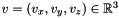$v=(v_x,v_y,v_z) \in \mathbb{R}^3$ , and the angular velocity 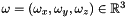$\omega=(\omega_x,\omega_y, \omega_z) \in \mathbb{R}^3$ . 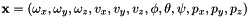The whole state of the helicopter is denoted by the 12-tuple $\mathbf{x} = (\omega_x,\omega_y, \omega_z, v_x, v_y, v_z, \phi, \theta, \psi, p_x, p_y, p_z)$ .

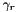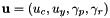The controls consist of the angles that control the main rotor by pitching it forward (pitch $\gamma_p$ ) and tilting it sideways (roll $\gamma_r$ ) 2 remaining inputs are the collective and (yaw)rudder forces so that $\mathbf{u} = (u_c, u_y, \gamma_p, \gamma_r)$ .

It is assumed that the center of mass (COM) lies directly below the main rotor, i.e. that the main rotor axis is aligned with the body fixed z-axis (with origin at the COM). Similar assumption is made about the rear rotor application point with respect to the negative body-fixed x-axis. The rear rotor produces rudder force in the y-axis direction. The default heli parameters are distance b/n COM and top rotor 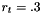$ r_t = .3 $ and distance b/n COM and rear rotor 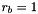$ r_b = 1 $ , mass 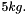$ 5 kg.$ . Moments of inertia can be taken from a comparable small RC helicopter but here we assume that the helicopter mass is concentrated in a sphere of radius rt/2 and mass mb fixed at the COM. Rotational moments of inertia are computed using the sphere as well as a a virtual disk or radius rb and weight mr representing the spinning top rotor fixed at distance rt above the COM perpendicular to the body-fixed z-axis.

Denote the whole configuration by 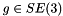$g \in SE(3)$ , the whole velocity by 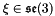$\xi \in \mathfrak{se}(3)$ , defined by

$\begin{align*} g = \left[\begin{array}{cc} R & p \\ \mathbf{0} & 1 \end{array}\right], \quad \xi = \left[ \begin{array}{cc} \widehat\omega & v \\ \mathbf{0} & 0 \end{array}\right]. \end{align*}$

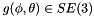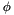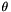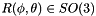Denote the transformation corresponding to roll and pitch only by $g(\phi,\theta) \in SE(3)$ . Denote a rotation corresponding to roll $\phi$ , and pitch $\theta$ by $R(\phi, \theta) \in SO(3)$ .

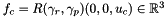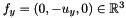Denoting the vectors $f_c = R(\gamma_r, \gamma_p) (0,0,u_c)\in \mathbb{R}^3$ and $f_y = (0, -u_y, 0) \in \mathbb{R}^3$ .

The control forces 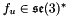$f_u \in \mathfrak{se}(3)^*$ acting on the system in its body frame are

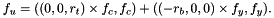
$\begin{align*} f_u = ((0,0,r_t) \times f_c, f_c) + ((-r_b,0,0) \times f_y, f_y). \end{align*}$

Now let's check what conditions are necessary for motion invariant to translations and rotations around the 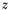$ z $ -axis, i.e. to 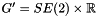$G^{\prime} = SE(2)\times \mathbb{R}$ transformations. This means that there is a velocity 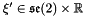$\xi^{\prime}\in \mathfrak{se}(2) \times \mathbb{R}$ , that can be expressed as 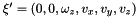$\xi^{\prime}=(0, 0, \omega_z, v_x, v_y, v_z)$ , for which 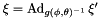$\xi = \operatorname{Ad}_{g(\phi,\theta)^{-1}}\xi^{\prime}$ is a relative equilibria for the whole system on 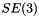$ SE(3) $ , i.e. 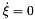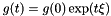$\dot \xi = 0$ and $g(t) = g(0)\exp(t\xi)$ .

This velocity is obtained by satisfying the invariance conditions

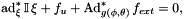
$\begin{align*} \operatorname{ad}_\xi^* \operatorname{\mathbb{I}} \xi + f_u + \operatorname{Ad}^{\ast}_{g(\phi,\theta)} f_{ext} = 0, \end{align*}$

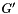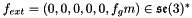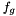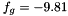using the $G^\prime$ -invariant external force $f_{ext} = (0,0,0,0,0,f_g m) \in \mathfrak{se}(3)^*$ with the scalar $ f_g $ denoting acceleration due to gravity (e.g. on Earth $ f_g=-9.81 $ ).

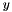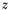These conditions can be simplified if one assumes that the moments of rotational inertia around the $ y $ and $ z $ axis are identical In this case the invariance requires that:

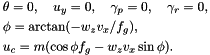
$\begin{align*} & \theta = 0, \quad u_y = 0, \quad \gamma_p = 0, \quad \gamma_r = 0, \\ & \phi = \arctan(-w_z v_x/f_g),\\ & u_c = m(\cos\phi f_g - w_z v_x \sin\phi). \end{align*}$

Constructor & Destructor Documentation

Heli::Heli ( )

References gcop::Body3d< 4 >::Bu, gcop::Body3d< 4 >::fp, and gcop::Body3d< 4 >::m.

Member Data Documentation

double gcop::Heli::rb

distance from center of mass to rear rotor (back)

Referenced by gcop::HeliView::Render().

double gcop::Heli::rt

distance from center of mass to main rotor (top)

Referenced by gcop::HeliView::Render().

The documentation for this class was generated from the following files:

lib/systems/heli.h
lib/systems/heli.cc

Public Member Functions

Public Attributes

Detailed Description

Constructor & Destructor Documentation

Member Data Documentation