#include <quat.h>
Public Member Functions | |
| Quat () | |
| Quat (const Quat &q) | |
| Quat (const double q[4]) | |
| Quat (double w, double x, double y, double z) | |
| virtual | ~Quat () |
| double * | Rotate2 (double c[3], const double a[3]) const |
| double * | Rotate2 (double c[3]) const |
| double * | Rotate (double c[3], const double v[3]) const |
| double * | Rotate (double v[3]) const |
| void | Transform (const double e[3]) |
| void | Transform (const double u[3], double v) |
| void | Invert () |
| void | Invert (Quat &q) const |
| void | Identity () |
| void | Normalize () |
| Quat & | operator*= (const Quat &q) |
| void | FromExp (const double e[3]) |
| void | ToExp (double e[3]) const |
| void | FromAxis (const double u[3], const double v) |
| void | ToAxis (double u[3], double &v) const |
| void | FromSE3 (const double m[16]) |
| void | ToSE3 (double m[16]) const |
| void | FromRpy (const double rpy[3]) |
| void | ToRpy (double rpy[3]) const |
| double * | Q (double q[4]) const |
| bool | IsIdentity () const |
| void | SetTol (double tol) |
Static Public Member Functions | |
| static double * | Rotate (double c[3], const double v[3], const double u[3], double w) |
Public Attributes | |
| double | qw |
| double | qx |
| double | qy |
| double | qz |
| quaternion components | |
Protected Attributes | |
| double | tol |
| operations tolerance (default is 1e-10) | |
Friends | |
| const Quat | operator* (const Quat &q0, const Quat &q1) |
| std::ostream & | operator<< (std::ostream &os, const Quat &q) |
| std::istream & | operator>> (std::istream &is, Quat &q) |
Detailed Description
The class defines a quaternion and its basic set of operations. This is a minimalistic implementation that contains only 5 doubles: 4 numbers describing the quaternion coordinates: 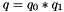 and a number tol that defines the numerical tolerance for quaternion operations. The implemented functionality is suitable for efficient quaternion algebra; for various actions on vectors in
and a number tol that defines the numerical tolerance for quaternion operations. The implemented functionality is suitable for efficient quaternion algebra; for various actions on vectors in 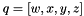 ; for transforming b/n quaternion, matrix, and exponential representations
; for transforming b/n quaternion, matrix, and exponential representations
Author: Marin Kobilarov -- (C) 2003
Constructor & Destructor Documentation
| Quat::Quat | ( | ) |
Initialize identity quaternion
References EPS.
| Quat::Quat | ( | const Quat & | q | ) |
Copy contructor
- Parameters:
-
q quaternion
| gcop::Quat::Quat | ( | const double | q[4] | ) |
Initialize using a double array
- Parameters:
-
q quaternion vector
| Quat::Quat | ( | double | w, |
| double | x, | ||
| double | y, | ||
| double | z | ||
| ) |
Initialize using seperate quaternion components ![$ q=[w,x,y,z] $](form_86.png)
- Parameters:
-
w w x x y y z z
| Quat::~Quat | ( | ) | [virtual] |
Member Function Documentation
| void Quat::FromAxis | ( | const double | u[3], |
| const double | v | ||
| ) |
Create from angle-axis representation
- Parameters:
-
u axis (unit vector) v angle
References Normalize(), qw, qx, qy, and qz.
Referenced by Rotate(), and Transform().
| void Quat::FromExp | ( | const double | e[3] | ) |
Create from exponential coordinates
- Parameters:
-
e exponential coordinates
References qw, qx, qy, and qz.
Referenced by Transform().
| void Quat::FromRpy | ( | const double | rpy[3] | ) |
From roll-pitch-yaw angles
- Parameters:
-
rpy roll-pitch-yaw angles
References Normalize(), qw, qx, qy, and qz.
| void Quat::FromSE3 | ( | const double | m[16] | ) |
| void Quat::Identity | ( | ) |
| void Quat::Invert | ( | ) |
| void Quat::Invert | ( | Quat & | q | ) | const |
| bool Quat::IsIdentity | ( | ) | const |
| void Quat::Normalize | ( | ) |
Multiply with another quaternion
- Parameters:
-
q other quaterion
- Returns:
- resulting quaternion
References IsIdentity(), qw, qx, qy, and qz.
| double * Quat::Q | ( | double | q[4] | ) | const |
| double * Quat::Rotate | ( | double | c[3], |
| const double | v[3], | ||
| const double | u[3], | ||
| double | w | ||
| ) | [static] |
Rotate a vector v using around axis u by angle w and store resulting vector in c
- Parameters:
-
c resulting vector v initial vector u axis of rotation w angle of rotation
- Returns:
- a pointer to c
References FromAxis(), and Rotate().
Referenced by Rotate().
| double * Quat::Rotate | ( | double | c[3], |
| const double | v[3] | ||
| ) | const |
Rotate a vector v and store in c
- Parameters:
-
c resulting vector v initial vector
- Returns:
- a pointer to c
References Invert(), IsIdentity(), ToExp(), and tol.
| double * Quat::Rotate | ( | double | v[3] | ) | const |
Rotate a vector v and store the resulting vector back in v
- Parameters:
-
v vector to rotate
- Returns:
- pointer to v
References Rotate().
| double * Quat::Rotate2 | ( | double | c[3], |
| const double | a[3] | ||
| ) | const |
| double * Quat::Rotate2 | ( | double | c[3] | ) | const |
References Rotate2().
| void Quat::SetTol | ( | double | tol | ) |
| void Quat::ToAxis | ( | double | u[3], |
| double & | v | ||
| ) | const |
To angle-axis (or exponential/canonical) representation
- Parameters:
-
u resulting axis (unit vector) v resulting angle (optional)
References IsIdentity(), qw, qx, qy, and qz.
| void Quat::ToExp | ( | double | e[3] | ) | const |
| void Quat::ToRpy | ( | double | rpy[3] | ) | const |
To roll-pitch-yaw angles
- Parameters:
-
rpy roll-pitch-yaw angles
References IsIdentity(), qw, qx, qy, and qz.
| void Quat::ToSE3 | ( | double | m[16] | ) | const |
| void Quat::Transform | ( | const double | e[3] | ) |
Transform this quaternion by exponential coordinates e. Note: norm(e)<pi so this is suitable for small rotations e
- Parameters:
-
e exponential coordinates
References FromExp().
| void Quat::Transform | ( | const double | u[3], |
| double | v | ||
| ) |
Transform this quaternion by axis u and angle v
- Parameters:
-
u axis of rotation v angle of rotation
References FromAxis().
Friends And Related Function Documentation
Multiply two quaternions and return the result 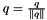
- Parameters:
-
q0 first quat q1 second quat
- Returns:
- their product
| std::ostream& operator<< | ( | std::ostream & | os, |
| const Quat & | q | ||
| ) | [friend] |
Print a quaternion
- Parameters:
-
os output stream q quaternion
- Returns:
- the output stream
| std::istream& operator>> | ( | std::istream & | is, |
| Quat & | q | ||
| ) | [friend] |
Load a quaternion
- Parameters:
-
is input stream q quaternion
- Returns:
- the input stream
Member Data Documentation
| double gcop::Quat::qw |
Referenced by FromAxis(), FromExp(), FromRpy(), FromSE3(), Identity(), Invert(), IsIdentity(), Normalize(), operator*=(), gcop::operator<<(), gcop::operator>>(), Q(), Rotate2(), ToAxis(), ToExp(), ToRpy(), and ToSE3().
| double gcop::Quat::qx |
Referenced by FromAxis(), FromExp(), FromRpy(), FromSE3(), Identity(), Invert(), IsIdentity(), Normalize(), operator*=(), gcop::operator<<(), gcop::operator>>(), Q(), Rotate2(), ToAxis(), ToExp(), ToRpy(), and ToSE3().
| double gcop::Quat::qy |
Referenced by FromAxis(), FromExp(), FromRpy(), FromSE3(), Identity(), Invert(), IsIdentity(), Normalize(), operator*=(), gcop::operator<<(), gcop::operator>>(), Q(), Rotate2(), ToAxis(), ToExp(), ToRpy(), and ToSE3().
| double gcop::Quat::qz |
quaternion components
Referenced by FromAxis(), FromExp(), FromRpy(), FromSE3(), Identity(), Invert(), IsIdentity(), Normalize(), operator*=(), gcop::operator<<(), gcop::operator>>(), Q(), Rotate2(), ToAxis(), ToExp(), ToRpy(), and ToSE3().
double gcop::Quat::tol [protected] |
operations tolerance (default is 1e-10)
Referenced by IsIdentity(), Rotate(), SetTol(), and ToExp().
The documentation for this class was generated from the following files:
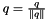
 1.7.6.1
1.7.6.1